Je suis sûre que c'est plus facile qu'avec une plume du Pilot Falcon

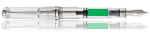

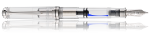
Madame n'est pas prof de mathHobiecat a écrit : J'ai donc fait la photo et le graphique, je te laisse calculer l'intégrale.
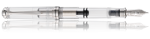
Ahh, j'aime beaucoup. Tu as bien réussi à capter son allure rapace. Superbe.grindsel a écrit :Allez, Hobiecat, un petit effort ...
Je suis sûre que c'est plus facile qu'avec une plume du Pilot Falcon


Je suis d'accord, mais aussi pour l'excellence des informations qu'on y trouve.Hobiecat a écrit :Toujours un plaisir de lire le fil du mardi pour la bonne humeur qui s'en dégage...
P'tète ben qu'c'est pour l'expression "schwa l'dire à ma mère", ben connue en Normandie, ou p'tète ben qu'non.borelek a écrit :En plus je me suis fait allumer au repas...ils ont prétendu que le mot schwa, les intégrales et les dérivées ne servaient à rien !
Même pour un simple calcul de poutre en béton armée, il faudrait résoudre une équation du 3ème degré, autrefois on avait des tables dans un grand livre. Quant aux magnifiques structures en résille à trois dimensions, qu'Alain nous a montrées, Je vous laisse imaginer le calcul matriciel nécessaire pour le calcul des efforts et moments dans chaque membrure à partir des 6 inconnues que constituent les déplacements et rotations de chaque nœuds dans un espace à 3 dimensions.Hobiecat a écrit :...Alain qui fait des jolies passerelles devrait être de ton côté : pour le calcul de ce genre de structure avec des charges réparties, il faut jouer un peu avec les intégrales (et donc avec les dérivées) si on veut que ça tienne.



Et bien tu vois borelek, au moins ça c'est clair...bebe a écrit :Je suis d'accord, mais aussi pour l'excellence des informations qu'on y trouve.Hobiecat a écrit :Toujours un plaisir de lire le fil du mardi pour la bonne humeur qui s'en dégage...P'tète ben qu'c'est pour l'expression "schwa l'dire à ma mère", ben connue en Normandie, ou p'tète ben qu'non.borelek a écrit :En plus je me suis fait allumer au repas...ils ont prétendu que le mot schwa, les intégrales et les dérivées ne servaient à rien !
Même pour un simple calcul de poutre en béton armée, il faudrait résoudre une équation du 3ème degré, autrefois on avait des tables dans un grand livre. Quant aux magnifiques structures en résille à trois dimensions, qu'Alain nous a montrées, Je vous laisse imaginer le calcul matriciel nécessaire pour le calcul des efforts et moments dans chaque membrure à partir des 6 inconnues que constituent les déplacements et rotations de chaque nœuds dans un espace à 3 dimensions.Hobiecat a écrit :...Alain qui fait des jolies passerelles devrait être de ton côté : pour le calcul de ce genre de structure avec des charges réparties, il faut jouer un peu avec les intégrales (et donc avec les dérivées) si on veut que ça tienne.
Pour le calcul des déplacements et rotations des extrémités d'une plume, c'est aussi un calcul matriciel avec F = K x D où F est le vecteur des sollicitations (efforts et moments suivant trois axes), et D est le vecteur des déplacements et rotations suivant ces trois axes. K est une matrice où l'on va retrouver les modules d'élasticité de Young et de Coulomb, et le coefficient de Poisson, ainsi que des termes compliqués à calculer, qui dépendent de l'inertie (épaisseur largeur longueur) mais aussi de la courbure et de la forme (pour aller plus loin, c'est bien expliqué ici).
On peut y arriver en découpant la plume en petits carrés (éléments finis), et en écrivant l'équation entre efforts et déplacements pour chaque coté de chaque carré. Si on fait alors la somme des déplacements, on obtient le vecteur des déplacements de la pointe fonction des efforts appliqués. Mais ça donne une matrice de 6 fois le nombre d’éléments finis au carré.
Dans les année 70, un ordinateur qui occupait 1 étage entier d'IBM, mettait une nuit pour inverser la matrice, et donner le résultat.




Relativise : moi, ils sont 14 (oui je sais, c'est peu ...) en face de moi, à me dire que les intégrales et dérivées ça ne sert à rien (à part les embrouiller et les enquiquiner ...). Et en plus, ils sont tous plus grands que moiborelek a écrit : En plus je me suis fait allumé au repas, à trois contre moi, ils ont prétendu que le mot schwa, les intégrales et les dérivées ne servaient à rien ! Hobiecat, tu trouverais pas une petite raffinerie dans la région d'Yverdon ? Je me sens un peu seul !
Ne dit-on pas aussi "j'vais l'dire à mon schwa'l" ?bebe a écrit :P'tète ben qu'c'est pour l'expression "schwa l'dire à ma mère", ben connue en Normandie, ou p'tète ben qu'non.
Mr Hobie ???Hobiecat a écrit :Mr Hobie n'a qu'à bien se tenir, tu vas lui faire de la concurrence avec ta marmotte géante !
Une petite révision des intégrales de Riemann ?Hobiecat a écrit : J'ai donc fait la photo et le graphique, je te laisse calculer l'intégrale.
Ah non, je refuse, Mme Einstein s'est déjà fait avoir avant moi, personne ne s'en souvient, il est hors de question que l'histoire recommencephilgood a écrit :Madame n'est pas prof de mathHobiecat a écrit : J'ai donc fait la photo et le graphique, je te laisse calculer l'intégrale.
Mr au photos, Mme aux calculs

C'est facile, quand la dérivée est positive, tu gagnes de l'argent, alors que quand elle est négative, tu en perds.Mrs Hobie a écrit :Personne pour me souffles des applications en économie des dérivées et intégrales, à part pour les valeurs moyennes, siouplé ?? ?


Pour en revenir au derivées et intégrale, le calcul de la matrix de raideur K typiquement utilise les deux concepts... surtout si on fait des elements finis. J'dis ca j'dis rienAlain146 a écrit :Et bien tu vois borelek, au moins ça c'est clair...bebe a écrit :Je suis d'accord, mais aussi pour l'excellence des informations qu'on y trouve.Hobiecat a écrit :Toujours un plaisir de lire le fil du mardi pour la bonne humeur qui s'en dégage...P'tète ben qu'c'est pour l'expression "schwa l'dire à ma mère", ben connue en Normandie, ou p'tète ben qu'non.borelek a écrit :En plus je me suis fait allumer au repas...ils ont prétendu que le mot schwa, les intégrales et les dérivées ne servaient à rien !
Même pour un simple calcul de poutre en béton armée, il faudrait résoudre une équation du 3ème degré, autrefois on avait des tables dans un grand livre. Quant aux magnifiques structures en résille à trois dimensions, qu'Alain nous a montrées, Je vous laisse imaginer le calcul matriciel nécessaire pour le calcul des efforts et moments dans chaque membrure à partir des 6 inconnues que constituent les déplacements et rotations de chaque nœuds dans un espace à 3 dimensions.Hobiecat a écrit :...Alain qui fait des jolies passerelles devrait être de ton côté : pour le calcul de ce genre de structure avec des charges réparties, il faut jouer un peu avec les intégrales (et donc avec les dérivées) si on veut que ça tienne.
Pour le calcul des déplacements et rotations des extrémités d'une plume, c'est aussi un calcul matriciel avec F = K x D où F est le vecteur des sollicitations (efforts et moments suivant trois axes), et D est le vecteur des déplacements et rotations suivant ces trois axes. K est une matrice où l'on va retrouver les modules d'élasticité de Young et de Coulomb, et le coefficient de Poisson, ainsi que des termes compliqués à calculer, qui dépendent de l'inertie (épaisseur largeur longueur) mais aussi de la courbure et de la forme (pour aller plus loin, c'est bien expliqué ici).
On peut y arriver en découpant la plume en petits carrés (éléments finis), et en écrivant l'équation entre efforts et déplacements pour chaque coté de chaque carré. Si on fait alors la somme des déplacements, on obtient le vecteur des déplacements de la pointe fonction des efforts appliqués. Mais ça donne une matrice de 6 fois le nombre d’éléments finis au carré.
Dans les année 70, un ordinateur qui occupait 1 étage entier d'IBM, mettait une nuit pour inverser la matrice, et donner le résultat.






Alors là , si il y a bien un truc que je déteste c'est de lire jusqu'à la fin...borelek a écrit :Alain, tu devrais lire mes messages jusqu'à la fin

Oui, d'accord, tu aurais pu dire : un forum intégralement dédié au stylo-plume, et ajouter aux produits dérivés.Alain146 a écrit :Ici c'est un forum de stylo-plume , alors on parle stylo-plume ! Uniquement stylo-plume , je te jure... t'en foutrai moi des intégrales dérivées, toujours les mêmes qui ne se font pas démoratiser ici...



bebe a écrit :Oui, d'accord, tu aurais pu dire : un forum intégralement dédié au stylo-plume, et ajouter aux produits dérivés.

Moi qui pensais être seul au mondeborelek a écrit :A quoi ça sert, les dérivées et les intégrales ? ça sert à être heureux.
Utilisateurs parcourant ce forum : Bing [Bot] et 4 invités